- Présentation des études
- Informations pratiques
- Les enseignements
- Informations officielles
- Outils
- Liens
- Master MEEF (Capes)
Cours de Nicolas Ressayre
Fondamentaux des mathématiques I
Cette page contient des informations relatives à l'UE Fondamentaux des mathématiques I, groupe MATH (séquences 5 et 1).
Pour les autres séquences, voir ici
Programme
Le programme de l'UE est disponible ici
Emploi du temps
L'UE se compose de 46h de cours magistraux, 64h de travaux dirigés et 24h d'études surveillées.
Les cours ont lieu le lundi matin (de 10h00 à 12h00) et le jeudi matin (de 10h00 à 12h00).
ATTENTION : pour des raisons de non disponibilité d'amphi, ces horaires sont susceptibles d'être modifiés. Seul ADE est fiable.
Les travaux dirigés ont lieu le mardi après-midi (3h) et le vendredi après-midi (2h30).
Les études surveillées (2h) sont organisées le lundi ou le jeudi matin, avant le cours. Deux enseignants y sont présents pour répondre aux questions sur les cours ou les TD. Il est fortement conseillé aux étudiants d'y assister.
Enseignants
Cours : M. Nicolas RESSAYRE mel
Travaux dirigés :
- Groupe A : Mme Véronique BATTIE mel
- Groupe B : M Pierre LAVAURS mel
- Groupe C : M Pascal LAINE mel
- Groupe D : M Octave LACOURTE mel
Études surveillées : M Pascal LAINE mel et M Alexis Tchoudjem mel
Ressources
Le site Exo7 contient une grande base d'exercices (avec indications et corrections) ainsi que des éléments de cours pour les étudiants en mathématiques à l'université ou en classes préparatoires.
Des exercices corrigés et des annales d'examen sont également disponibles ici (voir notamment les rubriques Maths I Analyse, Maths I Algèbre et Fondamentaux des mathématiques I).
Livre recommandé : ce cours téléchargeable est une bonne référence couvrant toutes les mathématiques de première année.
Modalités d'examen
L'UE comporte une partie de contrôle continu.
Calcul de la note finale d'UE :
(Examen final)*30% + Partiel*30% +[Examen 1 + Examen 2 + Examen 3 + Max(Examen1, Examen2, Examen 3)]*10%
Une absence injustifiée à une épreuve donne une note de 0.
Une épreuve de rattrapage permettra de remplacer une absence justifiée.
Le service de la scolarité du premier cycle est habilité à décider de la validité d'une justification.
Polycopié de Cours
Un polycopié est saisi par le chargé de cours à mesure que celui avance. Ce document est susceptible de contenir des erreurs et doit s'accompagner d'un présence en cours. Plus précisément le cours complète, corrige (le cas échéant), illustre et explique le document ( CoursFdM1).
Travaux dirigés
Feuille de TD no 1 ( Calculs algébriques). Corrigé
Feuille de TD no 2 ( Applications).
Corrigé
Feuille de TD no 3 ( Bases de logique).
Corrigé
Feuille de TD no 4 ( Fonctions usuelles).
Corrigé
Feuille de TD no 5 ( Nombres complexes).
Corrigé
Feuille de TD no 6 ( Suites réelles).
Corrigé
Feuille de TD no 7 ( Arithmétique).
Corrigé
Feuille de TD no 8 ( Limites et continuité).
Corrigé
Feuille de TD no 9 ( Polynômes).
Corrigé
Feuille de TD no 10 ( Dérivabilité).
Corrigé
Calendrier des Examens
Les dates inscrites sont celles des lundi. Certaines épreuves pourront être déplacées à un autre moment dans la même semaine.
Devoir Surveillé no 1 du lundi 7 octobre ( Questions préparées).
Devoir Surveillé no 2 du lundi 4 novembre( Sujet Corrigé).
Partiel du jeudi 21 novembre ( Sujet Corrigé).
Devoir Surveillé no 3 du jeudi 12 décembre( Sujet Corrigé).
Examen Final le Mercredi 18 décembre à 14h00 (durée 2h00) ( Sujet Corrigé).\\.
Oral de rattrapage pour ABJ à un DS : le jeudi 19 décembre entre 9h00 et 16h00.
Seconde chance le Jeudi 16 janvier à 11h30 (durée 1h00).
Déroulé du cours (du 12/9 au 16/12)
Chapitre I -- Calculs algébriques
Séance 1 (jeudi 12 septembre): Informations pratiques sur l'UE.
Nombres réels : définition comme écriture décimale, propriétés de +, x et ⇐ (existence admise), propriété de la borne supérieure (esquisse d'une preuve de l'existence), valeur absolue.
Séance 2 (lundi 16 septembre):
Sommes finis de nombres réels,
Changement d'indice, sommes télescopiques, produit de sommes.
Somme des n premiers entiers, n premières puissances, etc.
Coefficients binomiaux. Formule du triangle de Pascal. Formule du binôme de Newton.
Début du chapitre II : deux manières de décrire une partie d'un ensemble (paramétrique et implicite). Notation A l'ensemble des éléments de E qui vérifient une propriété. Intersection, union, complémentaire et lien avec les propriétés.
Chapitre II : Ensemble et Applications
Séance 3 (jeudi 19 septembre) : Exemples de preuves ensemblistes.
Applications d'un ensemble dans un autre (les ensembles de départ et d'arrivée sont donnés !) : exemples. On peut y penser comme une collections de flèches entre ensemble, un graphe, ou une collection d'étiquettes sur un ensemble 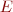 marquées avec les éléments d'un ensemble
marquées avec les éléments d'un ensemble 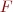 .
.
Séance 4 (lundi 23 septembre) : Injectivité, surjectivité, bijectivité : définition + interprétation sur les 3 “modèles” sus-cités. Composition : définition, exemple. Attention à l'ordre !
Chapitre III : Bases de la logique
Séance 5 (jeudi 26 septembre) : Logique : prédicat, opérations ou et implique et non. Quantificateurs. Un exemple de preuve pas disjonction de cas.
Séance 6 (lundi 30 septembre) : Finn du chapitre logique : 3 exemples de démonstration par récurrence usuelle et forte.
Chapitre IV : Fonctions usuelles
Séance 4 (lundi 23 septembre) : Début des fonctions usuelles : polynômes de degré 1 et 2, partie entière et fonctions trigonométriques.
Séance 6 (lundi 30 septembre) : Fonction exponentielle définie par l'équation différentielle (existence admise unicité démontrée). Mini formulaire : exp(-x), exp(x+y) (avec démo), dérivé, limites, allure du graphe.
Séance 7 (jeudi 3 octobre) : Fonction logarithme, puissances, limites comparées; convexité.
Chapitre V : Suites réelles
Séance 8 (lundi 7 octobre) : Définition de suites numériques, trois manières de se représenter une suite, suite monotone, bornée… Suites arithmétiques et géométriques. Suites définies par récurrence. Exemple de la suite de Héron.
Séance 10 (lundi 14 octobre) : Définition de limite. Exemples. Un second exemple historique de suites : méthode d'Archimède pour approcher pi. Unicité de la limite, convergente implique bornée.
Séance 12 (lundi 21 octobre) : Théorèmes sur les suites (avec preuves pour l'essentiel) : convergente implique bornée, somme de limites, produit de limites, quotient de limites, théorème des gendarmes.
Séance 14 (lundi 4 novembre) : Théorème des suites adjacentes, exemple de l'écriture décimale d'un nombre réel. Notion de suite extraite.
Séance 15 (jeudi 7 novembre) : Théorèmes de Bolzano-Weirstrass avec esquisse de preuve par dichotomie, Définition et opérations sur les limites infinies, Suites de Cauchy, preuve de l'équivalence Cauchy ssi connverge.
Chapitre VI : Retour sur l'exponentielle
Voir polycopié, non traité en cours.
Chapitre VII : Nombres Complexes
Séance 9 (jeudi 10 octobre) : Définition de nombre complexe, addition, multiplication, conjugaison, module, inversion.
Séance 11 (jeudi 17 octobre) : exponentielle complexe, décomposition polaire.
Séance 13 (jeudi 24 octobre) : racines n-ième, équations polynomiales de degré 2, D'alembert-Gauss. Formules pour transformations du plan.
Chapitre VIII : Arithmétique des entiers et des polynômes
Séance 16 (le jeudi 14 novembre) : nombres premiers (définition, infinité, test de primalité, crible d'Erathostène), décomposition en produit de nombres premiers (preuve de l'existence), pgcd (définition et algorithmes par décomposition en facteurs premiers et Euclide).
Séance 18 (le jeudi 21 novembre) : théorèmes de Bezout, Gauss, congruence et théorème chinois. Polynômes : définition, somme, évaluation, composé, dérivation…
Séance 20 (le jeudi 28 novembre) : Polynômes : division euclidienne. Racines d'un polynôme et multiplicité (def + avec dérivés).
Séance 22 (le jeudi 5 décembre) : Polynômes irréductibles, théorème de décomposition, Bezout, Gauss, Chinois.
Chapitre IX : Limites et continuité des fonctions de la variable réelle
Séance 17 (le lundi 18 novembre) : Définition de limites, exemples et règles de calcul. Définition de fonction continue.
Séance 19 (le lundi 25 novembre) : théorème des valeurs intermédiaires, fonction continue : injectivité et monotonie, sur un intervalle fermé et borné.
Séance 21 (le lundi 2 décembre) : prolongement par continuité. Dérivation : taux de variation, définition de nombre dérivé, de dérivabilité. Opérations : addition, produit, quotient, composée.
Chapitre X : Dérivation
Séance 23 (le lundi 9 décembre) : définition de droite tangente, dérivée de la réciproque (interprétation géométrique), Théorème de Rolle
Séance 24 (le jeudi 12 décembre) : Théorème des accroissements finis et corollaires (variation et dérivation).
Examens de l'an passé
Devoir Surveillé no 1 du ( Sujet Corrigé).
Devoir Surveillé no 2 du jeudi 8 novembre( Sujet Corrigé).
Partiel du jeudi 29 novembre ( Sujet Corrigé).
Devoir Surveillé no 3 du jeudi 8 décembre( Sujet Corrigé).
Examen Final de décembre 2018 ( Sujet Corrigé).
Sujet Session 2 de juin 2019 ( Sujet )